Cerjan Research Effort

Current Research

Local topological invariants

I have an active collaboration with Terry Loring at the University of New Mexico to develop and implement local topological invariants that are applicable to both tight-binding models, as well as realistic systems, such as photonic crystals. This work is based on using the "spectral localizer" to rigorously define a system's local topology. Broadly speaking, the spectral localizer is a method for performing dimensional reduction consistent with Bott periodicity, such that the topology of the fictitious dimensionally reduced system determines the local topology of the original system. In this way, this framework is able to reduce the topological classification of systems of any physical dimension and any Altland-Zirnbauer class to one of the three original invariants proposed by Kitaev, i.e., the partitioning of a system's spectrum about some gap for ℤ invariants, or the sign of a determinant or the sign of a Pfaffian for ℤ₂ invariants.

Recently, we developed a generalization of the spectral localizer framework that provides a complete approach for topologically classifying nonlinear materials, i.e., those described by a nonlinear Schrödinger equation. This has enabled us to provide a rigorous definition for topological solitons, as well as observe topological dynamics.

Bound states in the continuum

In an open system, a state is considered to be bound if all of the energy put into it remains spatially localized and does not radiate away to infinity. Conversely, a state for which any initial energy eventually will radiate away is called a resonance. Typically, a sufficient criteria for determining whether or not a state is bound is if its frequency lies within the continuum of frequencies available to the scattering channels; if the frequency lies outside of this continuum, the state is bound. However, it is possible to find radiationless states whose frequencies lie within the continuum of scattering channels. These peculiar modes have been coined bound states in the continuum (BICs), and exist in a range of different physical systems (a nice review can be found here).

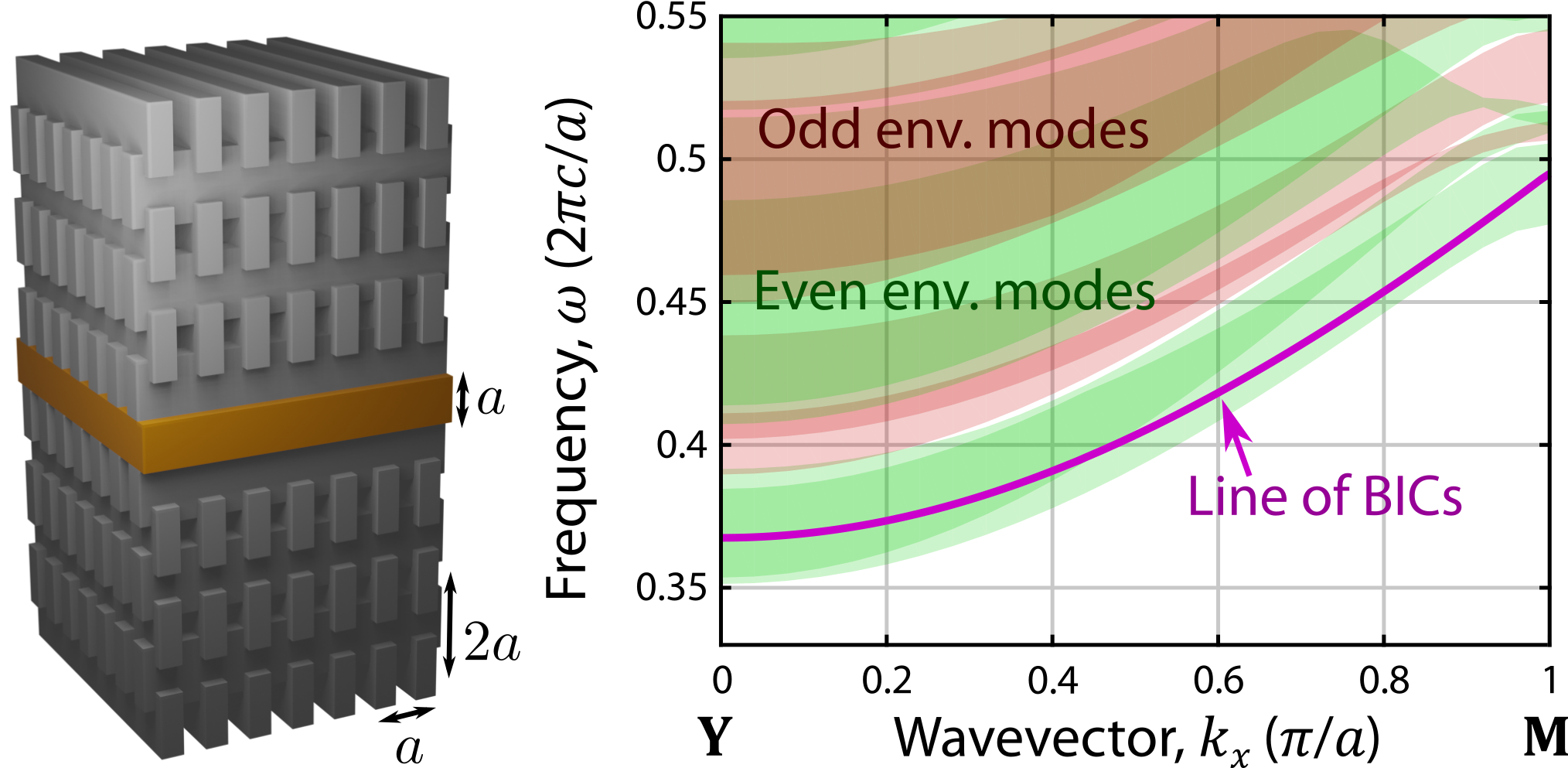
Previously, most studies of BICs focused on creating these bound modes by carefully engineering the device in which the BICs are spatially localized. However, in a recent work with Christina Jörg, we were able to use representation theory to prove that there are strong limitations on finding BICs that are protected by symmetry in planar photonic systems. Instead, we analytically and experimentally demonstrated that this limitation can only be overcome by changing the environment surrounding the device, rather than the device itself. In doing so, We also introduced the concept of a symmetry bandgap, a high-symmetry line or point in the Brillouin zone where the projected band structure only exhibits a subset of the allowed symmetries. This technique enables one to create continuous lines of symmetry-protected BICs in the system's Brillouin zone, an important property for future system design that had not been previously realized.

Now, working in collaboration with Igal Brener, Chloe Doiron, and Prasad P. Iyer, we are aiming to realize this physics in semiconductor photonic platforms.

Previous Interests

Prior to starting at Sandia, I completed my doctorate in physics with Douglas Stone at Yale University, spent two years working with Shanhui Fan at Stanford University, and three years working in Mikael Rechtsman's group at Pennsylvania State University.

Non-Hermitian Topological Photonics

Recently, there has been a great deal of interest in topological systems across many fields due to their ability to realize non-reciprocal transport even in the presence of disorder. Implicit in this statement is the assumption that both the underlying system and possible types of disorder are energy-conserving, i.e. Hermitian. However, one of the most important features of photonic systems is their ability to break Hermiticity through material gain or absorption, and through radiative outcoupling. This feature allows for the creation of lasers, for example, and more recently has enabled photonic systems to realize a variety of more exotic non-Hermitian phenomena, such as exceptional points. Given the potential uses of topologically protected transport in photonic devices, such as in optical interconnects, it is important to explore the consequences of non-Hermitian perturbations on topological systems, both to understand the limits of topological protection in the presence of gain and loss, but also to discover the new phenomena possible at the intersection of these two fields.

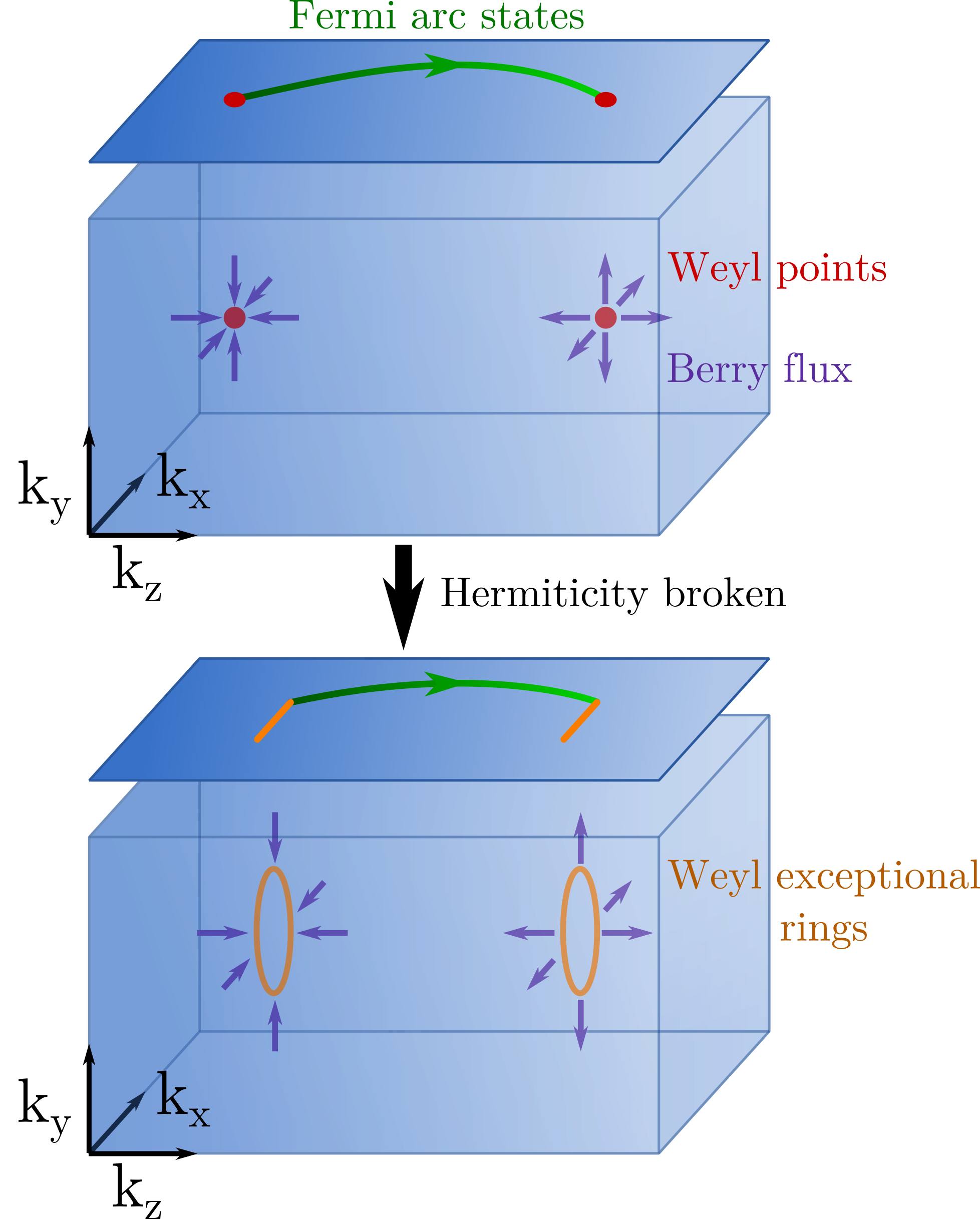
In my own work, I have made a few advances in the rapidly expanding field of non-Hermitian topological photonics. First, in collaboration with Prof. Shanhui Fan, I analytically proved that when gain and loss are added to Weyl materials, the Weyl points in the system's spectrum expand into one-dimensional contours of exceptional points, on which the Berry charge of the original Weyl point is exactly preserved. These topologically charged contours of exceptional points are called Weyl exceptional rings, and Fermi arc surface states still connect pairs of oppositely charged rings. Moreover, we then demonstrated that these Weyl exceptional rings allow for a new class of topological phase transition, as the strength of the non-Hermiticity is increased, rings with opposite charge can merge together, annihilating their Berry charge [ref].

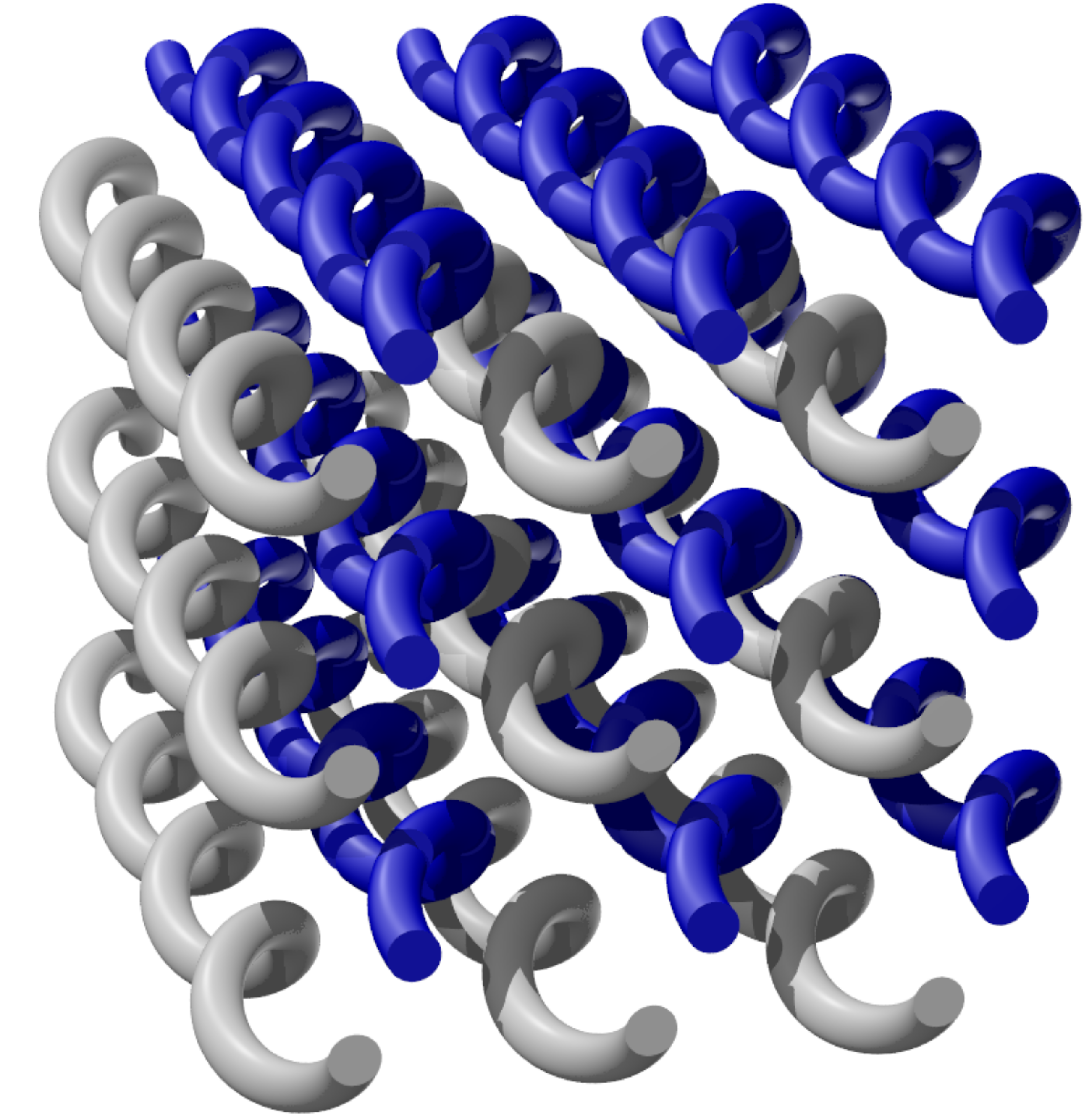
Then, in collaboration with Prof. Mikael Rechtsman, I experimentally realized the first Weyl exceptional ring in any system, using a helical waveguide array [ref]. To add the non-Hermiticity to the system, breaks were added to some of the waveguides, yielding a mechanism for tunable radiative out-coupling. It is also interesting to note that Weyl exceptional rings are the first known distributed source of Berry flux, which runs counter to the usual intuition that sources or sinks of Berry charge act like magnetic monopoles of Berry curvature in the Brillouin zone of a system.

Control over pairs of polarization states

As polarization is one of the fundamental properties of light, devices and materials which manipulate light's polarization are important for many applications, such as optical communication networks and sensors. Typically, given a particular input state of polarization, it is always possible to find a set of birefringent components which can rotate that initial state into any desired output polarization state. However, once this transformation is chosen, it completely determines the rotation of any input state. In particular, when using traditional (Hermitian) birefringent materials, this transformation always preserves the interior angle between any two polarization states.

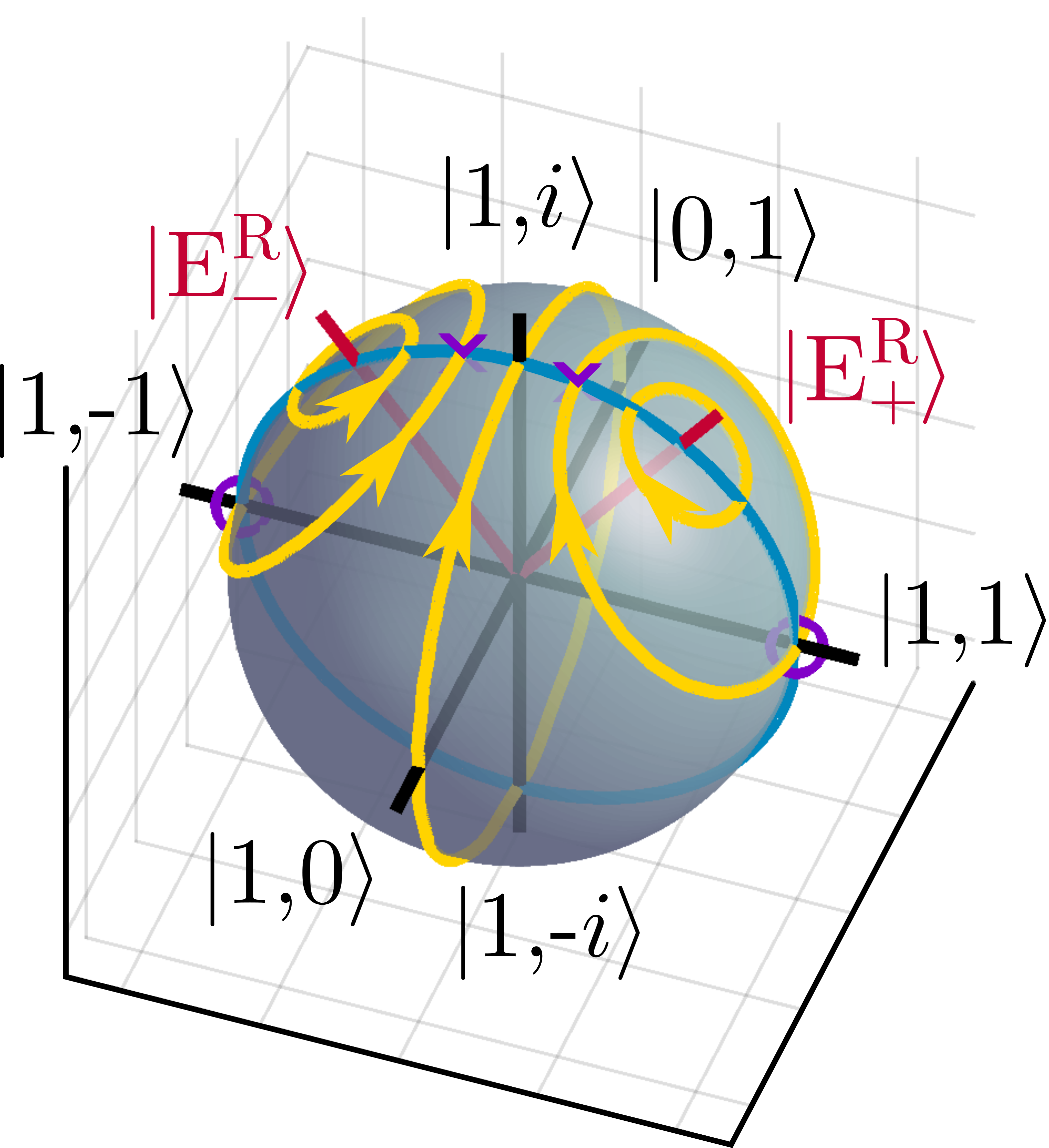
Instead, in collaboration with Prof. Shanhui Fan, I discovered that by using birefringent materials which also possessed gain and loss along different optical axes, we could manipulate pairs of input polarization states independently [ref]. These so called complex birefringent materials can realize both packing and separation of polarization states, and may have uses in new multiplexing schemes in optical communications. Moreover, the analytic theory underpinning these devices also shows how the eigenvectors of the dielectric tensor form an axis about which polarization flows on the Poincaré sphere, yielding an insightful method for visualizing these phenomena.

Developing and testing a theory of the quantum laser linewidth

Since the development of the quantum limited laser linewidth due to phase fluctuations from spontaneous emission events by Schawlow and Townes, many corrections have been subsequently discovered. Traditionally, these corrections have all been considered to be mutually independent, and include the Petermann factor, due to the non-orthogonality of the cavity modes, the incomplete inversion factor, and the bad-cavity correction, a linewidth reduction due to dispersion effects. Recently, a new method of calculating the intrinsic laser linewidth in terms of quantum fluctuations around the SALT steady- state was developed [ref], which demonstrated that the Petermann factor and bad-cavity corrections to the Schawlow-Townes linewidth are intertwined, and can only be separated in certain limits.

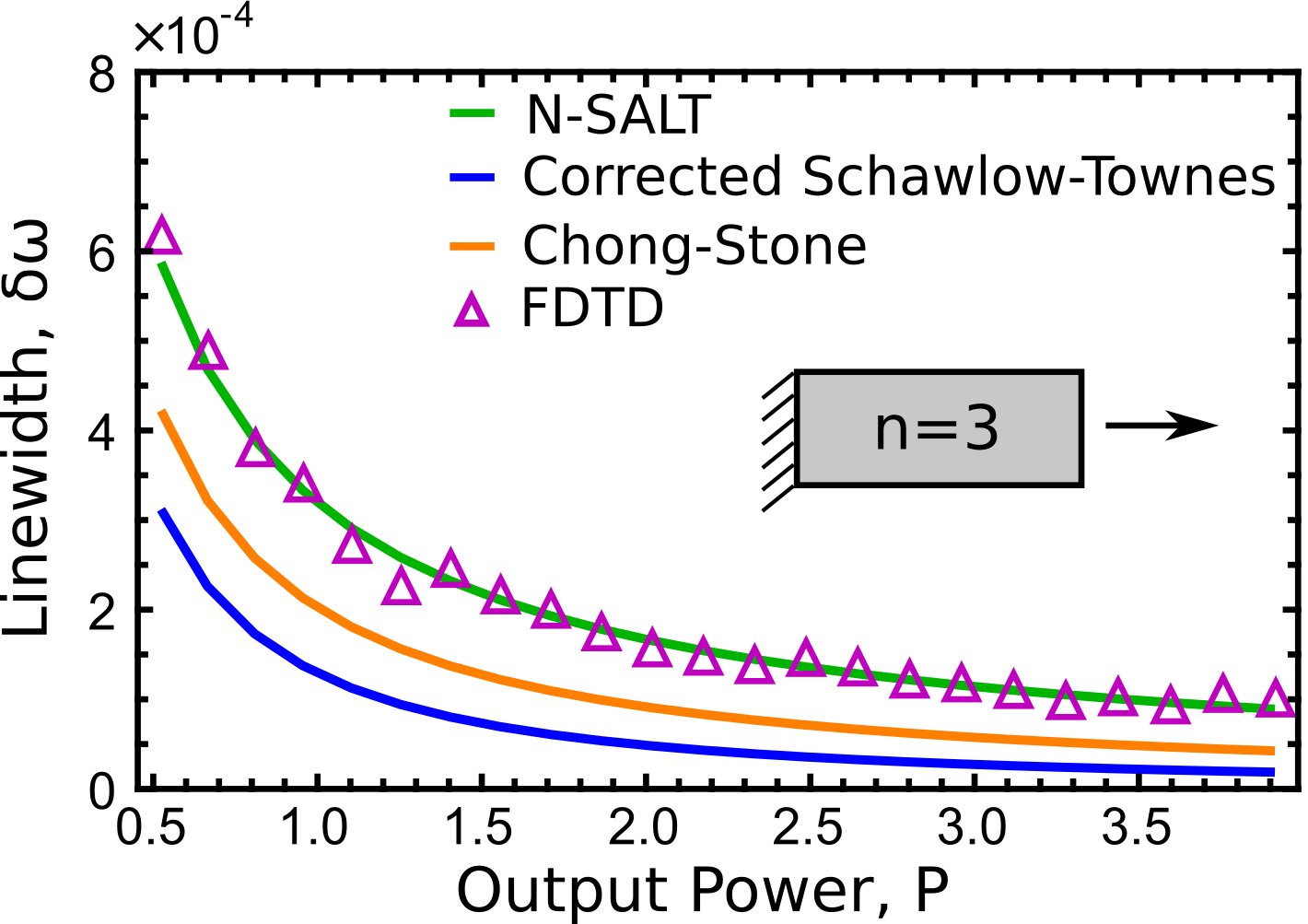
Following on this success, and in collaboration with Dr. Adi Pick and Profs. Steven Johnson and Douglas Stone, we were able to derive a complete analytic theory of the quantum-limited laser linewidth that inherently included all of the previously known corrections, again demonstrating that in general these effects are not simply multiplicative [ref]. This new theory also includes the Henry alpha-factor, which is a significant source of noise in semiconductor lasers. To verify this theory, I wrote a finite-difference time-domain (FDTD) code which simulated the Maxwell-Bloch equations coupled to the Langevin noise equations of the gain medium. Using this algorithm, we were able to quantitatively verify our analytical theory without the use of any fitting parameters [ref].